Krull–Schmidt category
In category theory, a Krull–Schmidt category is a generalization of categories in which the Krull–Schmidt theorem holds. They arise in the study of the representation theory of finite-dimensional algebras.
Contents |
Definition
Let k be a field. A category enriched over finite-dimensional k-vector spaces is a Krull–Schmidt category if all idempotents split. In other words, if 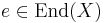 satisfies
satisfies 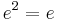 , then there exists an object Y and morphisms
, then there exists an object Y and morphisms 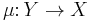 and
and 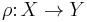 such that
such that 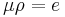 and
and 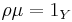 . If
. If 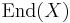 is a local ring whenever X is indecomposable, i.e., not isomorphic to the coproduct of two nonzero objects, then the condition is satisfied and the category is Krull–Schmidt.
is a local ring whenever X is indecomposable, i.e., not isomorphic to the coproduct of two nonzero objects, then the condition is satisfied and the category is Krull–Schmidt.
To every Krull–Schmidt category K, one associates a Auslander–Reiten quiver.
Properties
One has the analogue of the Krull–Schmidt theorem in Krull–Schmidt categories. Namely, given isomorphisms 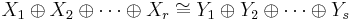 where the
where the 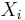 and
and 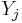 are indecomposable, then
are indecomposable, then 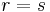 , and there exists a permutation
, and there exists a permutation  such that
such that 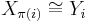 for all i.
for all i.
See also
References
- Claus Michael Ringel, Tame Algebras and Integral Quadratic Forms, Lecture Notes in Mathematics 1099, Springer-Verlag, 1984.